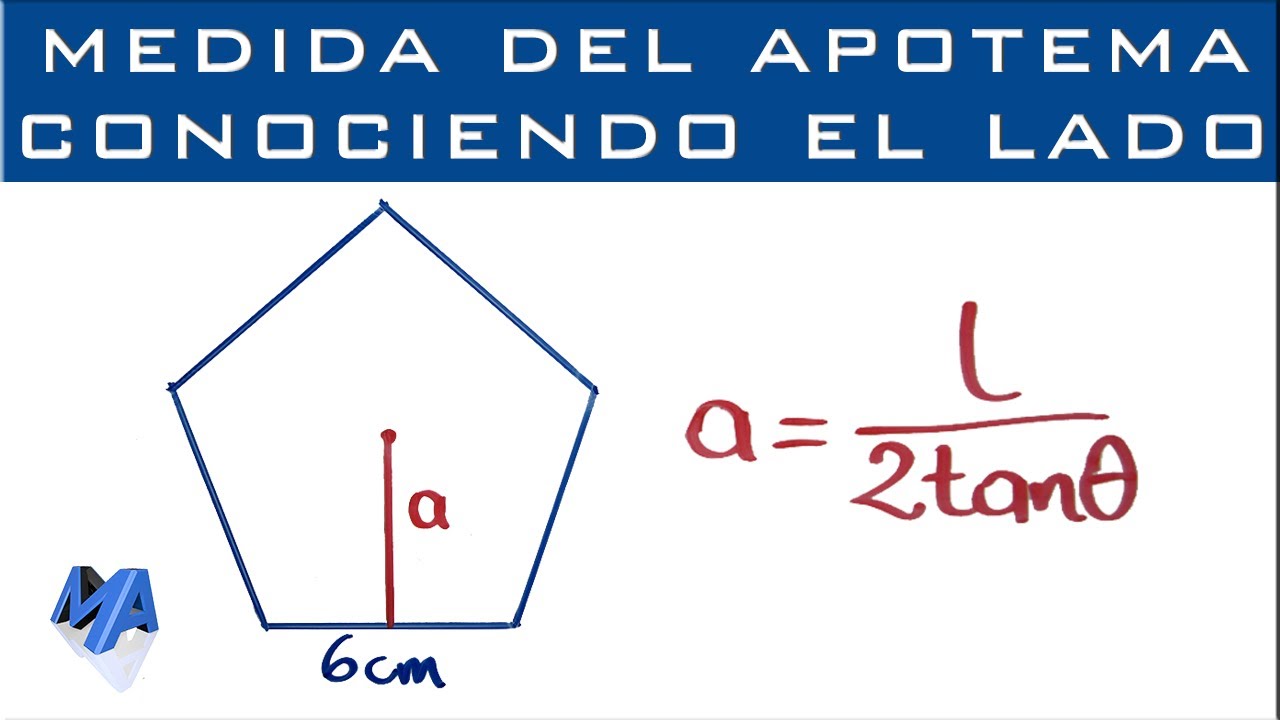
¿Qué es el apotema de un polígono regular?
El apotema de un polígono regular es una línea que se traza desde el centro del polígono hasta uno de sus lados, formando un ángulo perpendicular con ese lado. Esta línea divide al polígono en dos triángulos congruentes y tiene una longitud constante en todos los lados del polígono.
¿Cómo se calcula el apotema de un polígono regular?
El cálculo del apotema de un polígono regular depende del número de lados del polígono y de la longitud de los lados. Hay diferentes fórmulas para calcular el apotema, dependiendo de la información disponible. A continuación, explicaremos algunas de las fórmulas más comunes.
Fórmula del apotema en función del lado
Si conocemos la longitud de uno de los lados del polígono regular, podemos utilizar la siguiente fórmula para calcular el apotema:
Apotema = Lado / (2 * tan(π / N))
Donde “Lado” es la longitud del lado del polígono y “N” es el número de lados del polígono.
Esta fórmula se basa en la trigonometría y utiliza la función tangente para calcular el apotema en función de un ángulo determinado. En este caso, el ángulo es π / N, donde π (pi) es una constante matemática aproximadamente igual a 3.14159 y N es el número de lados del polígono.
Fórmula del apotema en función del radio
Si conocemos el radio del círculo circunscrito al polígono regular, podemos utilizar la siguiente fórmula para calcular el apotema:
Apotema = Radio * cos(π / N)
Donde “Radio” es el radio del círculo circunscrito al polígono y “N” es el número de lados del polígono.
Esta fórmula se basa en la trigonometría y utiliza la función coseno para calcular el apotema en función de un ángulo determinado. En este caso, el ángulo es π / N, donde π (pi) es una constante matemática aproximadamente igual a 3.14159 y N es el número de lados del polígono.
Ejemplos de cálculo del apotema de un polígono regular
Para ilustrar mejor cómo se calcula el apotema de un polígono regular, veremos algunos ejemplos con diferentes números de lados.
Ejemplo 1: Triángulo equilátero
Un triángulo equilátero es un polígono regular con tres lados de igual longitud. En este caso, podemos calcular el apotema utilizando la fórmula del apotema en función del lado:
Apotema = Lado / (2 * tan(π / 3))
Supongamos que el lado del triángulo equilátero mide 6 unidades. Sustituyendo en la fórmula:
Apotema = 6 / (2 * tan(π / 3))
Apotema = 6 / (2 * tan(1.047))
Apotema = 6 / (2 * 1.732)
Apotema ≈ 1.732 unidades
Por lo tanto, el apotema de un triángulo equilátero con un lado de longitud 6 unidades es aproximadamente 1.732 unidades.
Ejemplo 2: Cuadrado
Un cuadrado es un polígono regular con cuatro lados de igual longitud. En este caso, podemos calcular el apotema utilizando la misma fórmula del apotema en función del lado:
Apotema = Lado / (2 * tan(π / 4))
Supongamos que el lado del cuadrado mide 5 unidades. Sustituyendo en la fórmula:
Apotema = 5 / (2 * tan(π / 4))
Apotema = 5 / (2 * tan(0.785))
Apotema = 5 / (2 * 1)
Apotema = 5 / 2
Apotema = 2.5 unidades
Por lo tanto, el apotema de un cuadrado con un lado de longitud 5 unidades es 2.5 unidades.
Usos del apotema de un polígono regular
El apotema de un polígono regular tiene varios usos en diferentes áreas, como la geometría, la arquitectura y la ingeniería. Algunos de los usos más comunes incluyen:
Área de un polígono regular
El apotema de un polígono regular es necesario para calcular su área. La fórmula para calcular el área de un polígono regular es:
Área = (Perímetro * Apotema) / 2
Donde “Perímetro” es la suma de las longitudes de los lados del polígono y “Apotema” es la longitud del apotema.
Cálculo de volúmenes de sólidos
El apotema de un polígono regular también es importante en el cálculo de volúmenes de sólidos, como pirámides y prismas, que tienen una base poligonal regular. El cálculo del volumen de estos sólidos se basa en el área de la base del polígono y la altura, que se puede obtener utilizando el apotema.
Estabilidad de estructuras
En arquitectura e ingeniería, el apotema de un polígono regular también se utiliza para garantizar la estabilidad de las estructuras. Al conocer el apotema, se pueden calcular los ángulos de los elementos estructurales y garantizar que la distribución de la carga sea adecuada.
Preguntas Frecuentes
¿El apotema de un polígono regular siempre es menor que la mitad de la longitud del lado?
Sí, el apotema de un polígono regular siempre es menor que la mitad de la longitud del lado. Esto se debe a que el apotema forma un triángulo rectángulo con el lado del polígono, y según el teorema de Pitágoras, la hipotenusa del triángulo es siempre mayor que uno de los catetos. En este caso, el cateto es la mitad de la longitud del lado y el apotema es menor que la hipotenusa.
¿Se puede tener un polígono regular sin apotema?
No, todos los polígonos regulares tienen un apotema. El apotema es una característica fundamental de los polígonos regulares y está presente en todos ellos. Puede haber casos en los que el apotema sea muy pequeño o difícil de medir, pero siempre está presente.
¿Hay alguna relación entre el apotema y el radio del círculo circunscrito al polígono?
Sí, hay una relación entre el apotema y el radio del círculo circunscrito al polígono regular. En el caso de polígonos regulares, el apotema es igual al producto del radio y el coseno del ángulo formado por el radio y uno de los lados del polígono. Esta relación se utiliza en la fórmula del apotema en función del radio.